14 Exploratory Factor Analysis
This page is a work in progress, but I welcome early feedback.
14.1 Bottom Line Up Front
Exploratory Factor Analysis (EFA) is a technique to identify potential dimensions that may underlie many variables. It is related to dimension reduction techniques, such as Principal Components Analysis (PCA). There are two major hyperparameter decisions to make when conducting EFA: first is the choice of estimator and most often we’ll use Maximum Likelihood (ML) or Weighted Least Squares Means and Variances adjusted (WLSMV) estimators for continuous or categorical variables, respectively; second is the type of rotation where oblique approaches allow the underlying factors to correlate, and orthogonal rotation forces the factors to be uncorrelated. Oblique rotations are more realistic and factors are usually correlated in some way, but orthogonal rotation may make it easier to identify factors. A scree plot of eigenvalues helps to identify the appropriate number of factors along with visual inspection of the correlation matrix. Finally, a Confirmatory Factor Analysis (CFA) should be used to evaluate the factor structure after an EFA.
14.2 Key Concepts
In both descriptive and most inferential statistics, psychologists are predominantly concerned with the actual variables in their data set. These variables can include the presence of a behavioral outcome such as turnover in an organization or the conditions of an experimental manipulation such as the dose of a medication. These are observable behaviors or manifest_indicators of behavior. That is, I can see someone leave an organization, or I can count the number of participants in each experimental condition. However, psychologists also work with unobservable phenomena. We suspect there are underlying elements or latent_factors which drive observable behaviors. Taking this a step further, latent factor theory suggests our responses to assessments which typically have many manifest indicators, or items, are driven by latent factors. Consider personality for example. This theory suggests our trait-level of latent conscientiousness would impact our responses to questions about our typical level of orderliness, self-control, and attention to detail. An exploratory_factor_analysis (EFA) attempts to identify these latent factors and their relationships with each other. Finally, although the personality example above demonstrates the relationships between latent factors and manifest indicators, it’s important to note latent factors are not constructs; further validation evidence is necessary.
Psychologist’s assessments also tend to be complicated, leveraging many manifest indicators or items in their measurement. Therefore, EFA can also be consider a member of the family of dimension_reduction_techniques which are used to succinctly describe or quantify complex phenomena. Dimension reduction can be done explicitly by estimating participants standing on factor scores of the underlying dimensions. A related dimension reduction technique is principal_components_analysis (PCA) which should rarely be used in psychology or psychometrics but is useful in illustrating some key concepts to ensure EFA is easier to understand.
14.3 Hyperparameter Decisions
Hyperparameters are decisions made prior to the analysis. Suppose you’re about to drive to work and want to know the best route. You have a choice of apps and you feel Apple Maps offers the best ease of use, Google Maps offers reliability, and Waze has high resolution traffic, accident, and police information. You’re in a rush today and prioritize reliability and therefore chose Google Maps. All three are capable of giving you a route, but the choice made before opening an app is a hyperparameter decision. Just like this example, hyperparameter decisions are those made before going down the road of factor analysis.
14.3.1 Factor Extraction Method
The goal of any dimension reduction or factor analytic technique is to identify factors which account for some common variance across the items. A specific type of common variance is communality (\(h^2\)), which is a standardized estimate which ranges from 0 to 1, where 0 means no common variance where the factor accounts for no variability in observed scores and 1 is perfect or complete common variance meaning all variability in observed responses is 100% driven by the underlying factor. In PCA, common variance is the total variance, which is a very strong assumption and this is specifically why PCA should not typically be used. EFA distinguishes between common and unique variance, there the unique variance is \(1-h^2\).It basically means you perfectly measured with no measurement error or other source of unique variance in the observed scores. Generally the guidance is to reserve PCA for formative constructs such as socioeconomic status or for dimension reduction in machine learning.
Related is the concept of eigenvalues. A components or factors eigenvalue the proportion of total variance across the variables explained by that component. The greater the eigenvalue, the more common variance explained by that component or factor. The number of eigenvalues is the number of variables. Also note, PCA is usually based on correlation matrices, where variables are standardized with a variance of 1. So for 9 variables, each with variance of 1, the total variance is also 9 in a PCA. For EFA, the sum of the eigenvalues is the total common variance not including the unique variance, so the eigenvalues in EFA will always be smaller. The EFA approach to factor extraction better reflects the fact that variance in observed responses is attributable to both common variance and unique variance. In general, EFA should be preferred.
14.3.2 Estimator Choice
Another quasi-hyperparameter decision is the choice of estimator. It’s not technically a hyperparameter decision as the properties of the data should drive the choice of the estimator rather than preferences, but it is somewhat a hyperparameter decision as these rules are strong guidelines but up for debate and should be specified by the user. Returning to the Apple vs. Google Maps example, perhaps you tend to give more weight to Google’s green route feature instead of reliability and would let that factor drive your decision more than others would. This is much like researchers who give more weight to the literature which focuses on the applicability in one domain over another. In reality, academics and researchers tend to stick with the estimators they learned in graduate school.
An estimator is an algorithm or mathematical procedure to approximate some parameter based on sample data. Usually they will iterate or try multiple factor solutions which summarize the data and will pick the best estimate based on some criterion. One common estimator is the maximum_likelihood (ML) method which seeks to find the factor solution which makes the underlying observed covariances between variables in the dataset most probable. ML estimation is dependent on some stronger assumptions of the data, namely it assumes data are multivariate_normal and linear relationships between the observed variables and the underlying factors. ML estimation tends to work better with few outliers and struggles if there exists multicolinearity among the observed variables. Further, although not really an assumption, ML tends to perform better by providing more stable estimation with larger sample sizes. There are no hard and fast rules for what makes a larger sample size, but common recommendations encourage more than several hundred observations. Although it lacks robustness to violations of some of these assumptions, ML remains the preferred estimation method in EFA.
Returning to the quasi-hyperparameter decision, some have argued Likert-type responses commonly used in psychological assessments violate the normality assumption of the ML estimator in that they are categorical data and not continuous, although the number of response categories leaves this up for debate. Regardless of that debate, an alternative estimator is weighted_least_squares (WLS) estimation.
14.3.3 Rotation
In factor analysis, rotation refers to the technique used to extract factors. There are many different types of rotation, but the fall into two camps: oblique vs. orthogonal. An oblique rotation means that extracted factors are allowed to be correlated after rotation. Promax and oblimin are common oblique rotation methods. Promax is the most frequently used oblique rotation method, often preferred due to its computational efficiency. Oblimin rotation allows for correlation between factors but aims to minimize the complexity of the pattern.
in orthogonal rotation, factors remain uncorrelated. Varimax and quartimax are common orthogonal rotation methods. Varimax maximizes the variance of the squared loadings within each factor, making the loadings on each factor clearer and simpler. Quartimax aims to minimize the number of factors required to explain each variable.
There are justifications for using either type of rotation, most tend to stick with what they were taught in grad school, but each has one major, strong argument; those in the oblique rotation camp suggest this better reflects reality as most latent factors tend to be correlated to some degree, and therefore the orthogonal rotation which assumes zero correlation between extracted factors is too strong and unrealistic an assumption. Those in the orthogonal camp argue uncorrelated factor solutions makes for easier interpretation of factor loadings, and the truth of the factor intercorrelation can be later confirmed using Confirmatory Factor Analysis (CFA).
14.3.4 Extraction Criteria
The ultimate goal of EFA is to determine the number of underlying factors that adequately describes the relationships between the observed variables. To determine what is ‘adequate’ is up to debate as different analysts have different criteria, and even after over 100 years of factor analysis there are no perfect criteria. Still, this hyperparameter decision necessitates we choose some criteria before analysis. For a moment, consider how criteria might differ in another setting, like talent scouts at a baseball game using different criteria to evaluate the best player they can recruit. One may think the best player is one who scores more runs than should be expected, another may compare the relative contribution of a player’s runs to the total game score, and another may use sophisticated software to compare a player’s performance to some other random player.
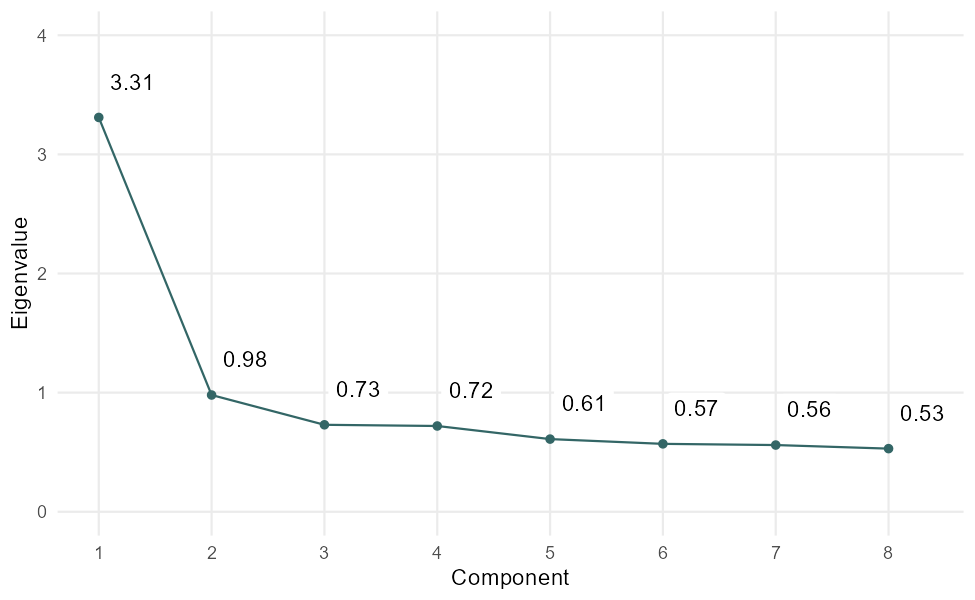
Keeping these different scouts in mind, let’s return to extraction criteria in EFA. There are three main types of extraction criteria: Kaiser criteria which focus on the eigenvalues of the components or the factors, Scree plot inspection, and parallel analysis. Kaiser criteria focus on eigenvalues that are greater than one. Recall in PCA, at least, the variances are standardized, so an eigenvalue greater than one means the component is accounting for more variance than just one item alone, and a value less than one means the component is accounting for less than even one variable and should be discarded. This is like the first talent scout. This arbitrary rule makes perfect sense mathematically, but breaks down in EFA contexts as the eigenvalue no longer represents the proportion of total variance but only the common variance attributable to the squared factor loadings; simply, we expect it to be lower than PCA eigenvalues. Therefore, we may, and often do, still have meaningful factors under this arbitrary threshold.
A second commonly used criterion is the scree plot (Cattel, 1966). The scree plot technique takes all the eigenvalues, orders them from highest to lowest
14.4 Exploratory Factor Analysis (EFA)
14.4.1 An Abstract Example
Factor analytic techniques assume the observed scores on an assessment are comprised of the impact of the latent factor level plus some uniqueness:
\[ X = ΛF + Ψ \]
Where:
- \(X\): Data matrix of observed variables (n observations x p variables).
- \(Λ\): Matrix of factor loadings (n x k), where k is the number of factors.
- \(F\): Matrix of latent factors (k x p).
- \(Ψ\): Matrix of unique factors or error terms (n x p).
The matrix form of this equation can be a little complicated, so we can also represent this factor by factor:
\[ x_i = λ_{i1}f_1 + λ_{i2}f_2 + ... + λ_{ik}f_k + ψ_i \]
Where:
- \(x_i\): Score of the \(i\)th observed variable.
- \(λ_{ij}\): Loading of the \(i\)th observed variable on the \(j\)th factor.
- \(f_j\): Score of the \(j\)th latent factor.
- \(k\): Number of factors.
- \(ψ_i\): Unique factor or error term for the ith observed variable.
This format can still be a bit complicated, so to make things a bit simpler, consider the formulas below for a two factor model:
\[ x_i = λ_{i1}f_1 + λ_{i2}f_2 + ψ_i \]
Where:
- \(x_i\): Score of the \(i\)th observed variable.
- \(λ_{i1}\): Loading of the \(i\)th observed variable on the 1st factor \(f_1\).
- \(λ_{i2}\): Loading of the \(i\)th observed variable on the 2nd factor \(f_2\).
- \(f_1\): Score of the first latent factor.
- \(f_2\): Score of the second latent factor.
- \(ψ_i\): Unique factor or error term for the \(i\)th observed variable.
To make this a little more concrete, consider a personality measure which is based on two latent factors, one factor driving responses to items assessing conscientiousness, and another factor underlying emotional stability items, corresponding to factor 1 and factor 2, respectively.
Then consider responses to this item: I am always prepared. This is a conscientiousness item, one highly correlated with the latent factor, represented by a high factor loading on factor 1 (\(λ_{i1}\)). We would expect someone who is high on conscientiousness in terms of their standing on the latent factor (\(f_1\)) to also have a high observed rating on this item (\(x_i\)) and vice versa. Considering the other terms, assuming conscientiousness and emotional stability are uncorrelated, so the factor loading associated with the latent emotional stability factor (\(λ_{i2}\)) should be low, meaning someone’s standing on the emotional stability latent factor (\(f_2\)) should be irrelevant to their observed score. Now consider an emotional stability item: I am relaxed most of the time. For this item, observed scores are driven by the factor 2 loading (\(λ_{i2}\)) and the person’s standing on the factor (\(f_2\)).
14.5 References
Beavers, A. S., Lounsbury, J. W., Richards, J. K., Huck, S. W., Skolits, G. J., & Esquivel, S. L. (2013). Practical considerations for using exploratory factor analysis in educational research. Practical Assessment, Research, and Evaluation, 18(1), 6.
Cattell, R. B. (1966). The scree test for the number of factors. Multivariate behavioral research, 1(2), 245-276.
Costello, A. B., & Osborne, J. (2005). Best practices in exploratory factor analysis: Four recommendations for getting the most from your analysis. Practical assessment, research, and evaluation, 10(1), 7.
Fabrigar, L. R., Wegener, D. T., MacCallum, R. C., & Strahan, E. J. (1999). Evaluating the use of exploratory factor analysis in psychological research. Psychological methods, 4(3), 272.
Gerbing, D. W., & Hamilton, J. G. (1996). Viability of exploratory factor analysis as a precursor to confirmatory factor analysis. Structural Equation Modeling: A Multidisciplinary Journal, 3(1), 62-72.
Hayton, J. C., Allen, D. G., & Scarpello, V. (2004). Factor retention decisions in exploratory factor analysis: A tutorial on parallel analysis. Organizational research methods, 7(2), 191-205.
Henson, R. K., & Roberts, J. K. (2006). Use of exploratory factor analysis in published research: Common errors and some comment on improved practice. Educational and Psychological measurement, 66(3), 393-416.
Horn, J. L. (1965). A rationale and test for the number of factors in factor analysis. Psychometrika, 30, 179-185.
Hurley, A. E., Scandura, T. A., Schriesheim, C. A., Brannick, M. T., Seers, A., Vandenberg, R. J., & Williams, L. J. (1997). Exploratory and confirmatory factor analysis: Guidelines, issues, and alternatives. Journal of organizational behavior, 667-683.
Kline, R. B. (2023). Principles and practice of structural equation modeling. Guilford publications.
MacCallum, R. C., Widaman, K. F., Zhang, S., & Hong, S. (1999). Sample size in factor analysis. Psychological methods, 4(1), 84.
Russell, D. W. (2002). In search of underlying dimensions: The use (and abuse) of factor analysis in Personality and Social Psychology Bulletin. Personality and social psychology bulletin, 28(12), 1629-1646.
Yong, A. G., & Pearce, S. (2013). A beginner’s guide to factor analysis: Focusing on exploratory factor analysis. Tutorials in quantitative methods for psychology, 9(2), 79-94.
14.6 Working Notes
Maximum likelihood estimation is preferred
The eigenvalues in EFA are sum of the squared factor loadings
FA based “eigenvalues” are always going to be lower than PCA-based ones
Maximum likelihood estimation is preferred
The eigenvalues in EFA are sum of the squared factor loadings across the factors.
Correlated latent factors and orthogonal (uncorrelated) latent factors
In one medical research paper, Proitsi et al. (2009) write:
“The WLSMV is a robust estimator which does not assume normally distributed variables and provides the best option for modelling categorical or ordered data (Brown, 2006)”.
Brown, T. (2006). Confirmatory factor analysis for applied research. New York: Guildford.