Inferential Statistics
Frequentist Statistics
Most people who use psychological statistics adopt a #frequentist approach which views probabilities in terms of the frequency of events over many trials. Imagine conducting the same experiment over and over again, frequentist statistics looks at how often certain outcomes would occur in the long run. For example, if we were to say the probability of flipping a coin and it landing on tails is 50%, the frequentist perspective would base this claim on many repeated coin flips, perhaps hundreds or even thousands.
A key concept in frequentist statistics is hypothesis testing. Recall the difference between a #population, a #sample, and a #sampling_distribution from [[Statistics]], hypothesis testing attempts to make inferences about the nature of populations based on their samples. For example, supposed we wanted to test the average height difference between men and women, suspecting that men were taller on average than their female peers. The frequentist approach is to take the average heights of samples repeatedly and create a sampling distribution of the average height difference between men and women. In reality, we don’t actually take multiple samples, but frequentists assume multiple samples, instead using the #maximum_likelihood estimation (MLE) to find the values for population parameters that make the statistic in our observed data most probable. It’s a way to estimate the parameters that best fit the data within a given statistical model.
Frequentist statistics has been a dominant paradigm in many scientific disciplines for decades, providing a useful framework for making statistical inferences. Its emphasis on objective, repeatable procedures and reliance on long-run frequencies have contributed to its widespread use in experimental and observational studies. However, it also faces criticisms, such as its dependence on large-sample assumptions and its limited handling of uncertainty. The other major approach to statistics is Bayesian statistics. In #bayesian_statistics, probability is interpreted as a measure of belief or uncertainty, allowing researchers to update their beliefs based on both prior knowledge and new evidence. Unlike frequentism, which relies on long-run frequencies, Bayesian statistics incorporates the researchers understanding of probabilities about the likelihood of events. Both approaches offer distinct advantages and each have their own disadvantages, but given the simplicity of the frequentist perspective as well as it’s ubiquity in education and training programs, frequentist statistics are much more commonly used. ## Null Hypothesis Significance Testing (NHST) The frequentist perspective adopts a formal approach to hypothesis testing as a decision tool. The most common statistical decision tool in psychology to establish differences between groups or the strength of a relationship between variables is #null_hypothesis_significance_testing(NHST). NHST starts with a null hypothesis, specifically, that there are no statistically significant difference between groups or the relationships between variables is not strong enough to be statistically significant. This null hypothesis is abbreviated \(H_0\). Researchers then posit an alternative to the null hypothesis, the alternative hypothesis \(H_a\) or \(H_1\) to suggest there is a meaningful group difference or relationship. Researchers will test some inferential statistical method and if the test suggests statistical significance they will then reject the null hypothesis in support of the alternative hypothesis.
It’s important to be careful about rejecting the null hypothesis because we can be wrong and our research may suggest a statistically significant result which doesn’t really exist. This can lead to important decisions based on flawed research which are often very difficult to reverse even after the faulty research has been corrected. Therefore, researchers should be cautious about rejecting the null hypothesis. Rejecting the \(H_0\) when it is in reality true is referred to as a #type_i_error (type one error) or the #false_positive rate. In psychology, the standard Type I Error rate is referred to as \(\alpha\) and we accept we conduct a statistical test a null hypothesis will be erroneously rejected about 5% of time. Less critical but still important is the #type_ii_error rate (\(\beta\); type two error), which is the circumstance where we retain the null hypothesis when it should have been rejected; that is, a #false_negative. We expect this will happen about 20% of the time. This also means that we expect to correctly reject the null hypothesis 80% of the time, and this is referred to as #statistical_power (1-\(\beta\)) or our ability to detect statistically significant results when they are really present. However, the opposite is not true; a lack of power is not evidence there is no effect in reality. Post-hoc power analysis assumes there is an effect and should be generally avoided.
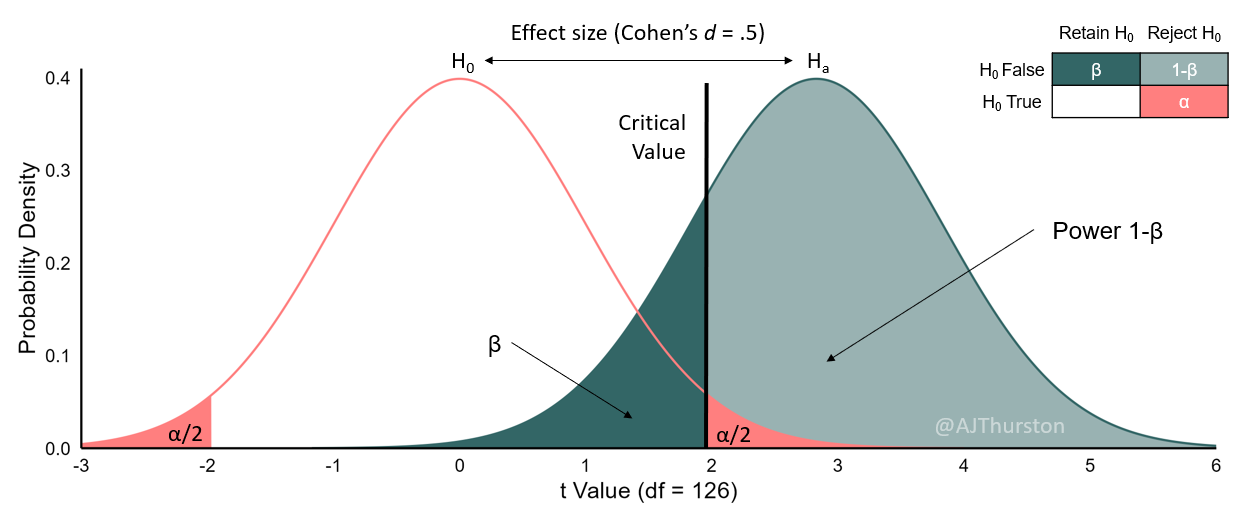
Statistical significance
The result of a statistical significance (s.s.) test is is typically expressed as a #p-value, which represents the probability of obtaining results as extreme as the ones observed by chance, assuming the null hypothesis is true. The decision to reject the null hypothesis is at p < .05; that is, if the p-value output from our statistical software is less than .05, we reject the null hypothesis in support of the alternative hypothesis. Note this is a somewhat arbitrary decision of about 2 standard deviations (1.96) above the mean of zero (Fisher, 1934). Some other scientific fields, such as physics and engineering, will have much higher thresholds. Although there is plenty of debate as to the value of statistical significance testing, to be discussed later, this is the standard within psychology.
Note, however arbitrary this standard, it is widely accepted, and deviations from this standard will invite skepticism and enthusiastic critique. For example, some will try to argue that p = .051 is “trending towards significance” or “marginally significant.” Some (e.g., Fisher, 1971) have argued NHST should not be a binary decision rule, and “marginally significant results” should encourage further experimentation, perhaps with stronger experimental conditions or manipulations. In reality, researchers who use this language are typically less interested further experimentation and more interested in papering over non-significant results for the purposes of publication. In the real world, psychology researchers using NHST should treat it as a single, dichotomous standard; either the results are statistically significant or they are not.
Critics of NHST will also argue, accurately and fairly, that NHST can lead to misinterpretation of results and narrow our focus to statistical significance rather than practical significance or effect size. Specific criticisms of NHST including the arbitrary setting of the null at zero and the tendency for significant results based on statistical power. Another flaw is #p-hacking where researchers will continue to increase sample size until a small effect size becomes statistically significant. Critics emphasize the importance of considering effect sizes and confidence intervals alongside NHST for a more comprehensive understanding of results, along with visual or graphic displays of data, better standardization of measurement (Cohen, 1994).
Other critiques look beyond the reformation of NHST and instead suggest turning to other alternatives entirely, such as Effect Size Testing (EST) and Bayesian methods. Bayesian methods in particular offer a robust set of tools to address the limitations of NHST by explicitly incorporating previously known information into the tests rather than testing against zero effect size. However, just like p-hacking, these methods can also be gamed, with more arbitrary decision rules than NHST, and sometimes less clear solutions as simple is reporting effect size and sample size.
Cortina and Landis (2001) argue that any translation of numbers into a verbal description will require some artificial categorization. Overall, they advocate improving how hypotheses are specified so that results can be better evaluated and communicated regardless of the statistical approach used. Another factor that should be considered is simply chance results, and that authors should discuss this explicitly. Despite the flaws of NHST, there are simple solutions in place that can compensate for these flaws, including better reporting. Although issues persist, and alternatives also have their own issues, are often much more complicated, and would require a sea change in education and training in psychological statistics with only some incremental added value. Simply put, statistical significance testing seems here to stay despite its issues. ## Effect size Although statistically significant results are the standard for NHST, scientists should also concern themselves with practical significance. Practical significance refers to the real-world importance or meaningfulness of some sort of treatment of relationship identified through research. Even though a result is statistically significant, it doesn’t necessarily mean it’s practically important. For example, we may find a statistically significant relationship between a training intervention and an important job-related outcome, but perhaps this s.s. result was due to chance or a large sample size. If it doesn’t actually improve people’s outcomes we might just be doing some statistical navel-gazing.
What is practically significant is a matter of interpretation, so statisticians’ role is to quantify practical significance and provide context. The #effect_size refers to how we quantify the magnitude of an observed effect or relationship in a study, that is, it’s practical significance. Effect sizes can be unstandardized, meaning in the units of the measure itself, or standardized, meaning units are based on the standard normal distribution, with a mean of zero and standard deviation one. Standardized effect sizes allow us to compare differences or relationships that may have been measured on different scales. Consider the following example below:
| Scenario 1 | Scenario 2 | |
|---|---|---|
| \(m_1\) | 10.40 | 119.00 |
| \(m_2\) | 8.90 | 79.00 |
| \(sd_1\) | 1.79 | 75.60 |
| \(sd_2\) | 3.85 | 84.09 |
| \(m_1-m_2\) | 1.50 | 40.00 |
| Cohen’s \(d\) | 0.50 | 0.50 |
Statistical significance, effect size, and sample size
Beyond detecting p-hacking, researchers using psychological statistics should understand the relationships between sample size, effect size, and p-values. Typically, these discussions focus on the minimum necessary sample size to determine the statistical significance of a particular effect size as in an #a_priori_power_analysis. Holding effect size constant, as sample size increases the p-value decreases and is more likely to become statistically significant. In many large samples, even trivial effect sizes are statistically significant. The same relationship is true if we instead hold sample size constant; as effect size increases, the p-value will also decrease. Even in studies with very small sample sizes, whoppers of effect sizes will be statistically significant.
Consider a simple example using the difference in means between two independent groups. Assuming equal sample sizes between these groups (\(n_1 = n_2\)), standardized group variances (\(\sigma = 1\)), and using the normal distribution, the formula for calculating the necessary sample size to establish statistically significant difference between two groups is: \[ \large n = \frac{2 \cdot (Z_{\alpha/2} + Z_{\beta})^2 }{\delta^2} \] Where: - \(n\) is the sample size per group, rounded up to the nearest integer. - \(Z_{\frac{\alpha}{2}}\) is the critical value corresponding to the significance level \(\frac{\alpha}{2}\): \(Z(.025) = 1.96\). - \(Z_{\beta}\) is the critical value corresponding to the chosen power level (\(1 - \beta\)): \(Z(.80) = .84\). - \(\delta\) is the standardized mean difference (effect size), usually Cohen’s d.
Note the effect size in the denominator. This means as the effect size increases the sample size necessary to detect it and establish statistical significance decreases. Working through a couple examples demonstrates the relationship better illustrates this point. Suppose we are conducting a study where we expect to detect a medium effect size of Cohen’s d = .5. Using the formula above: \[ \large n = \frac{2 \cdot (Z_{\alpha/2} + Z_{\beta})^2 }{\delta^2} = \frac{2 \cdot (1.96 + .84)^2 }{.5^2} = \frac{15.68}{.25} = 62.72 \] Using the typical inputs for power and alpha level, this solves for 62.72, but since we can’t have .72 of a participant in a study we always round up, in this case 63. Note, this is per group in this two group comparison, so we would need a total minimum sample size of 126 to achieve statistical significance if there was a standardized difference in the means between theses two groups at .5. Now examine what sample size would be required to achieve statistical significance give a small effect size of Cohen’s d = .1: \[ \large n = \frac{2 \cdot (Z_{\alpha/2} + Z_{\beta})^2 }{\delta^2} = \frac{2 \cdot (1.96 + .84)^2 }{.1^2} = \frac{15.68}{.01} = 1568 \]
Note how nothing changes in the denominator as we used the same alpha level and statistical power standards, but the comparatively smaller effect size dramatically increased the sample size for each group to detect such a small effect size. This would require over three thousand participants in a study to detect so small an effect size. Therefore, researchers can either increase the sample size or focus on larger effect sizes in order to achieve statistical significance. Usually reporting all three of these elements is preferred for transparency’s sake, so that other researchers or lay users of our research have all the information they need to understand how we reached our conclusions.
While this simplified formula was used to illustrate the relationship between sample size, effect size, and statistical significance, researchers rarely use these formula to determine necessary sample sizes directly. This formula uses the Z statistic to approximate the t statistic, which slightly underestimates the sample size necessary to detect the effect size. It’s more common to used Student’s t distribution directly, but is more complicated. Further, determining the sample size for this test, as well as many others, depends on factors like the ratio of the sample sizes between groups and the type of statistical test. Power analysis tools like G*POWER (Faul et al., 2007), or R packages and web tools like pwr and pwrss (Bulus, 2023) will account for these factors and provide better sample size estimates.
Bayes Theorem
| Background | ||||
|---|---|---|---|---|
| B | ¬B (not B) | Total | ||
| A | P(¬B|A)·P(A) = (A|¬B)·P(¬B) |
P(¬B|A)·P(A) = P(A|¬B)·P(¬B) |
P(A) | |
| Proposition | ¬A | P(B|¬A)·P(¬A) = P(¬A|B)·P(B) |
P(¬B|¬A)·P(¬A) = P(¬A|¬B)·P(¬B) |
P(¬A) = 1−P(A) |
| Total | P(B) | P(¬B) = 1−P(B) | 1 |